Warum die Infraschalldrücke der BGR falsch sind

Die für Windenergieanlagen berechneten Schalldrücke der BGR liegen um Größenordnungen über den Schalldrücken anderer Institutionen. Die Veröffentlichungen der BGR sind daher für viele Windkraftgegner so etwas wie der "heilige Gral". Sie liefern Argumente gegen Repowering und Vergrößerung von Windparks. Außerdem sagen sie beeindruckende Infraschall-Reichweiten von bis zu 50km voraus. Die angegebenen Schalldrücke der BGR sind so hoch, dass physiologische und psychologische Effekte denkbar wären. 

Tatsächlich sind die hohen Schalldrücke der BGR das Ergebnis eines Rechenfehlers. Dies möchte ich auf dieser Seite für Wissenschaftsinteressierte erläutern.

1. Was ist Schall?

Als Schall bezeichnet man periodische Druckschwankungen. Diese Druckschwankungen werden durch Frequenz und Amplitude beschrieben. Die in Herz (1Hz == 1 Schwingung pro Sekunde) gemessene Frequenz bestimmt die Tonhöhe. Die Amplitude wird in Pascal (1Pa ~ 100g/m²) angegeben und legt die Lautstärke fest. Je nach Frequenz unterscheidet man zwischen Infraschall (<20Hz), hörbarem Schall (20-20.000Hz) und Ultraschall (>20.000Hz). Die Einteilung ist vom menschlichen Hörvermögen abgeleitet und wird oft überinterpretiert. Eigentlich gibt es keine klaren Grenzen. Physikalisch betrachtet gibt es nur eine Form von Schall. Es gibt keinen Grund, warum sich ein 19Hz Ton grundlegend von einem 21Hz Ton unterscheiden soll. Menschen können auch Infraschall hören, wenn er entsprechend laut ist.

Die folgende Grafik zeigt das Drucksignal von zwei verschiedenen Tönen. Die schwarze Linie hat eine Amplitude von 0,1Pa und eine Frequenz von 50Hz, die rote Linie eine Amplitude von 0,05Pa und 19Hz. Das "rote Signal" wäre damit schwächer und tiefer als das "schwarze Signal".

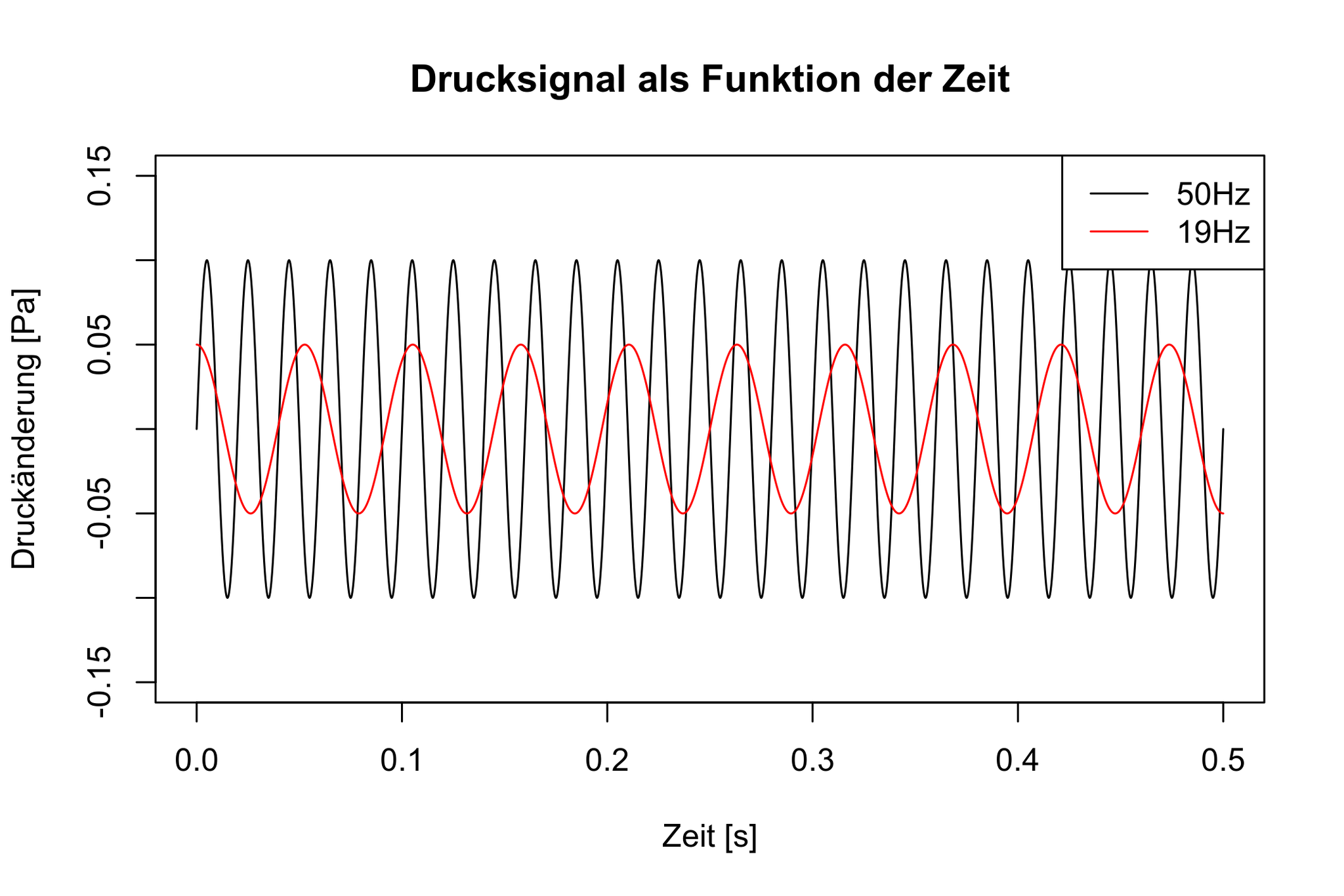
Abbildung 1: Beispiel für zwei reine Sinustöne

2. Schalldruckpegel - Dezibel (dB)

Da die Schallamplitude viele Größenordnungen (von einigen µPa bis mehrere 10er Pa) überspannen kann und das menschliche Hörempfinden nicht linear ist, ist es üblich, Lautstärken in einer logarithmischen Verhältnisskala anzugeben. Dies ist der sogenannte Schalldruckpegel, oft auch nur Schallpegel oder Lautstärke genannt. Der Schalldurckpegel wird aus der Amplitude wie folgt berechnet (Formel aus Wikipedia):

L p = 10 log 10 ⁡ ( p ~ 2 p 0 2 ) d B = 20 log 10 ⁡ ( p ~ p 0 ) d B {\displaystyle L_{\mathrm {p} }=10\,\log _{10}\left({\frac {{\tilde {p}}^{2}}{{p_{0}}^{2}}}\right)\,\mathrm {dB} =20\,\log _{10}\left({\frac {\tilde {p}}{p_{0}}}\right)\,\mathrm {dB} } .

  p ~ {\displaystyle {\tilde {p}}}ist dabei der Effektivwert des Schalldrucks. p₀ der Bezugswert, beim Luftschall wird p₀ = 20 µPa = 2·10⁻⁵ Pa verwendet.

Mit diesen Angaben können wir den Schalldruckpegel der beiden Signale von Abbildung 1 berechnen:

1. Schwarzes Signal (50 Hz Ton): 20·log₁₀(0,1 / √2 / 2·10⁻⁵) = 71dB
2. Rotes Signal (19 Hz Ton): 20·log₁₀(0,05 / √2 / 2·10⁻⁵) = 65dB

Die √2 kommt durch die Umrechnung der Amplitude in den Effektivwert in die Formel. Elektriker kennen diesen Faktor von der Wechselspannung. Eine 230V Wechselspannung hat eine Amplitude von √2 · 230V. Die übliche Abkürzung für Schalldruckpegel ist SPL (eng. Sound Pressure Level). Oft wird dB-SPL-Angaben noch der Zusatz "re 20µPa" hinzugefügt, um die Bezugsgröße deutlich zu machen.

3. Überlagerung von mehreren Signalen

Natürlich hat man es nie mit reinen Sinussignalen zu tun. Alle vorhandenen Signale müssen sich ein Medium (Luft) teilen und überlagern sich zu einem Summensignal. Nimmt man nur die beiden Signale aus dem ersten Plot, würde sich das folgende Summensignal ergeben:

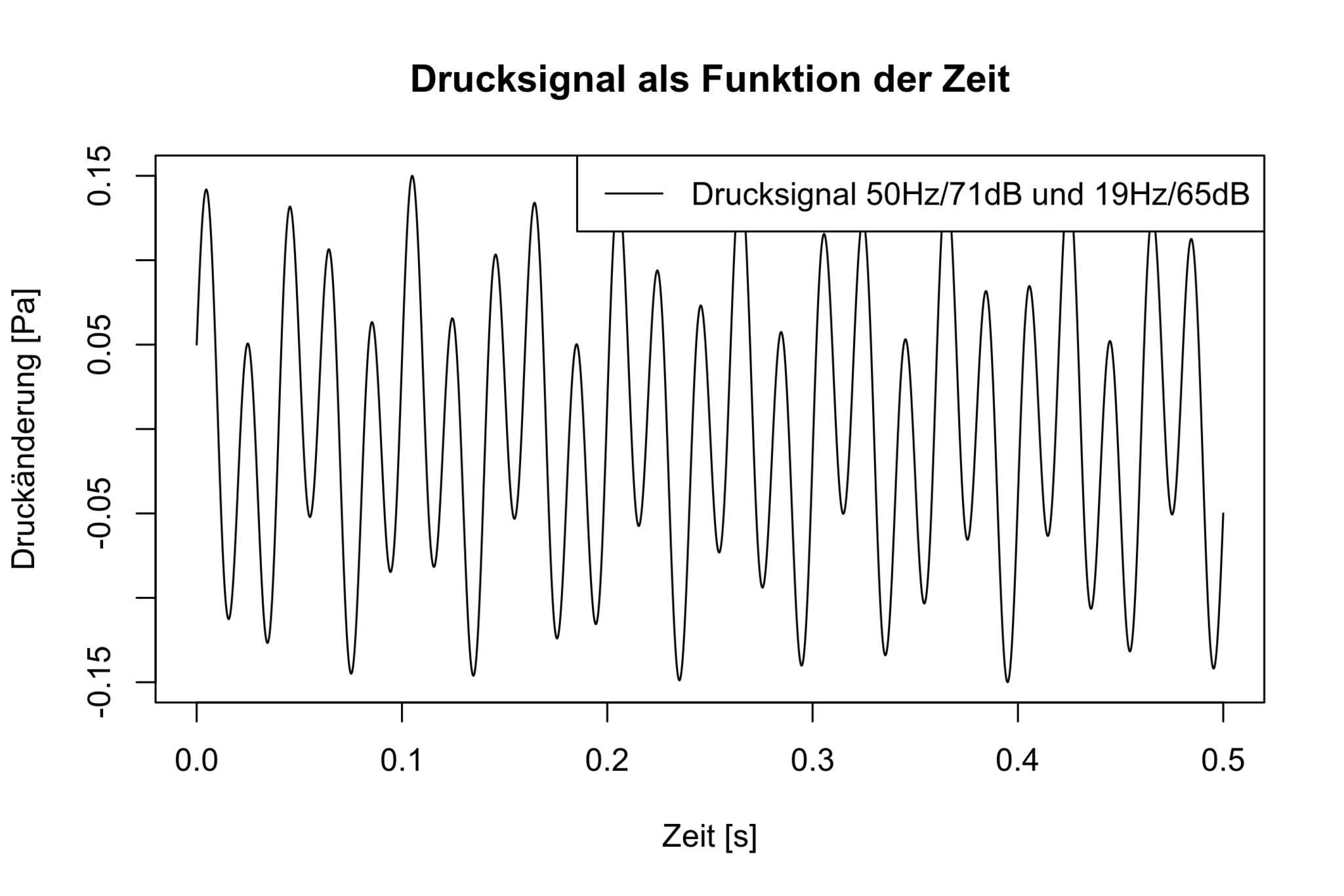
Abbildung 2: Exemplarisches Summensignal das sich aus der Überlagerung der beiden Sinus-Signale von Abbildung 1 ergibt.

Mit dem mathematischen Verfahren der Fourier-Transformation lassen sich aus diesem Drucksignal Amplitude und Frequenz der Einzelsignale extrahieren. Dabei kann der Gesamtpegel wie folgt berechnet werden (Gleichung aus Wikipedia):

10^(L_i/10) ist nichts anderes als  _i²/p₀². Daher ist die Summe in der Klammer die Quadratsumme der Einzelschalldrücke normiert auf die Bezugsgröße. Folglich muss auch der Gesamtpegel in dB immer größer sein als der größte Einzelpegel in dB. Für unsere beiden Signale zusammen ergibt sich somit ein Gesamtpegel von

10·log₁₀(10^(71/10)+10^(65/10) ) =  72dB.

Den gleichen Wert kann man berechnen, wenn man das Signal quadriert, mittelt und die Wurzel zieht (RMS - Root Mean Square).

Zur groben Abschätzung kann man auch die Peak-Amplitude (~0,15Pa) des Signals nehmen und mit den Formeln für reine Sinussignale den Schalldruck abschätzen:

20·log₁₀(0,15 / √2 / 2·10⁻⁵) = 74,5dB

Diese Abschätzung führt in der Regel zu einer Überschätzung (hier 2,5dB) des tatsächlichen Gesamtpegels.

4. Drucksignal der BGR-Messungen

Die folgende Abbildung zeigt das Drucksignal, welches in 200m zum Windrad und bei einer Umdrehungsgeschwindigkeit von 26 U/min aufgenommen wurde (Ceranna 2009, Abbildung 2):

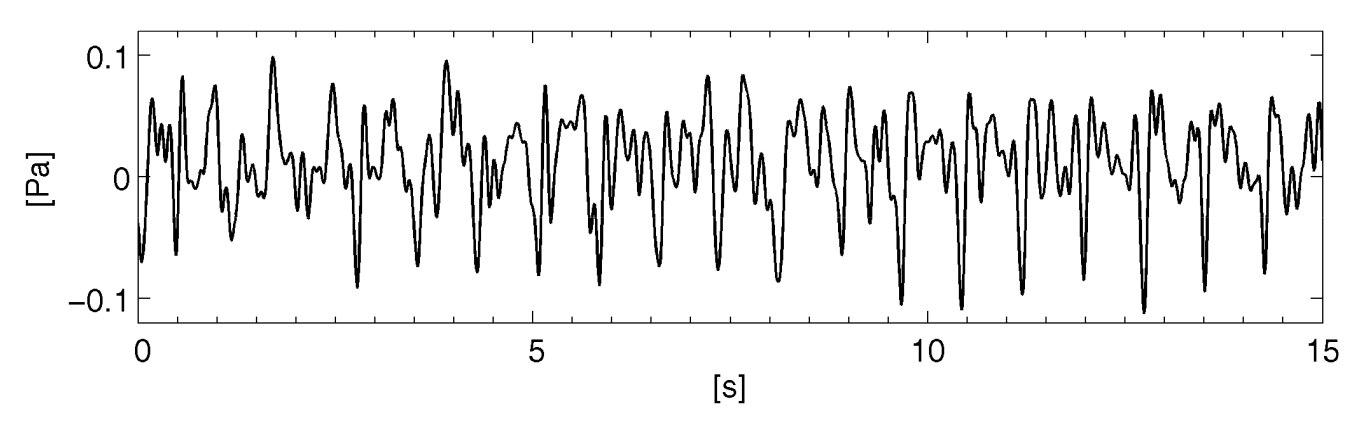
Abbildung 3: Drucksignal einer Windenergieanlage in 200m Abstand mit 0,5Hz Hochpassfilter (Ceranna 2009, Abbildung 2)

Nutzen wir die theoretischen Ausführungen vom vorherigen Abschnitt, können wir über die Amplitude (ca. 0,08Pa) den Gesamtpegel mit

20·log₁₀(0,08 / √2 / 2·10⁻⁵) = 69dB

grob abschätzen. Der tatsächliche Pegel dürfte noch ein paar dB niedriger liegen.

5. Schalldruckangaben (SPL) der BGR

Etwas weiter im Text (Ceranna 2009, Abbildung 5) findet man die folgende Grafik. Die Punke sind die Schalldruckpegel der 2. Flügeldurchgangsharmonischen (2. BPH == Einzelsignal) für verschiedene Standorte und Zeitpunkte (unterschiedliche Umdrehungsgeschwindigkeiten des Windrads), die aus dem primären Drucksignal errechnet wurden.

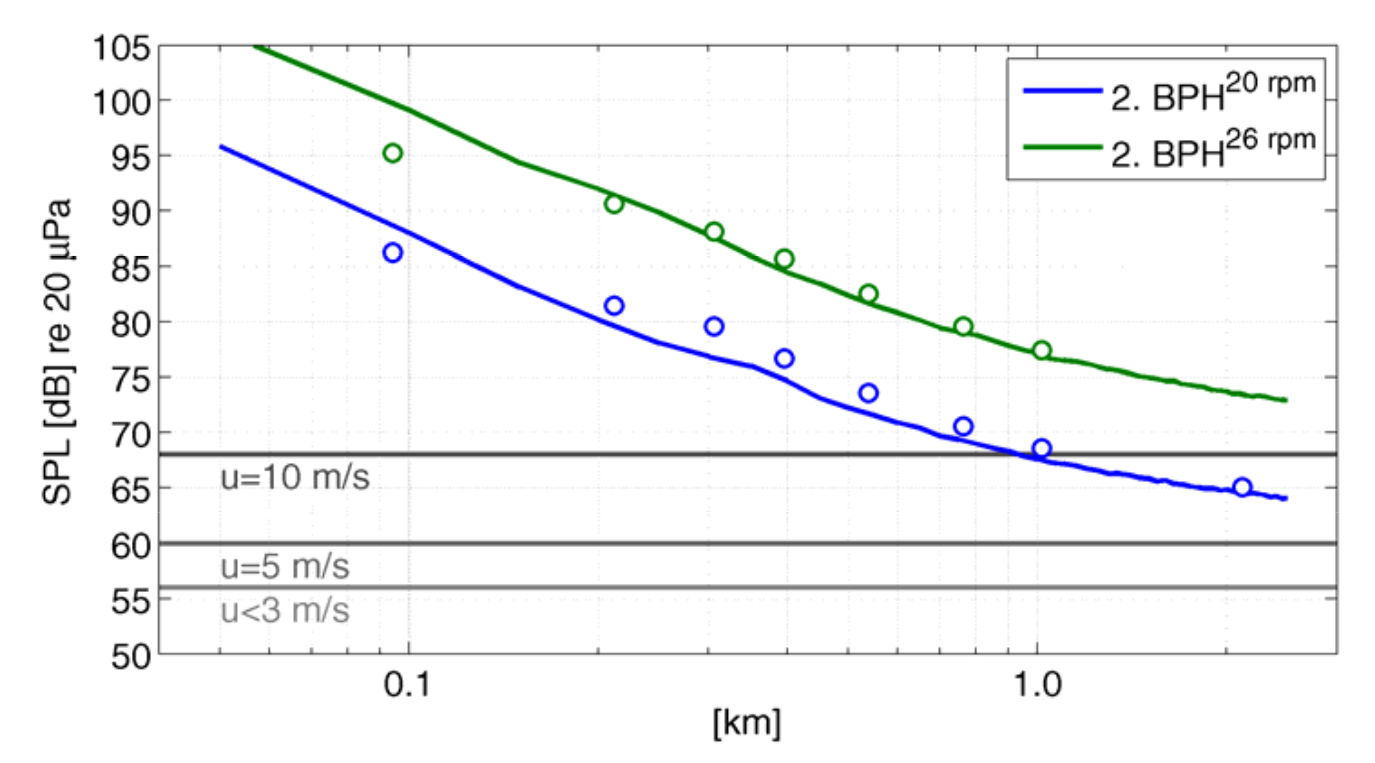
Abbildung 4: Entferungsabhängigkeit des Schalldruckpegels der 2. BPH (Flügeldurchgangsharmonischen) einer Vestas V47 (Ceranna 2009, Abbildung 5)

Ganz besonders interessiert uns der grüne Punkt bei 0,2km. Dieser Punkt entspricht hinsichtlich Abstand und Umdrehungsgeschwindigkeit den Bedingungen des zuvor gezeigten Drucksignals. Laut dieser Grafik soll der Schalldruck der 2. BPH etwas mehr als 90dB betragen!

Ich fasse zusammen:

1. Der Gesamtpegel ist <69dB
2. Der Gesamtpegel ist die RMS-Summe der Einzelpegel und ist immer größer als der größte Einzelpegel
3. Die BGR errechnet einen Einzelpegel (2.BPH) mit >90dB

Das ist eine physikalische Unmöglichkeit!!

Die primäre Messgröße ist das Drucksignal. Dieses passt gut zu Messungen anderer Institutionen und ist sicherlich korrekt. Damit ist es eindeutig, dass bei den SPL-Berechnungen der BGR ein gravierender Rechenfehler vorliegt. Der Rechenfehler dürfte in der Größenordnung von 30dB liegen. Bezogen auf den Energiegehalt ist dies ein Faktor 1000!

6. Modellrechnungen beinhalten den Rechenfehler

Das BGR hat basierend auf den falschen Schalldruckwerten Modellrechnungen für stärkere Windräder und Windparks aufgestellt (Ceranna 2009, Abbildung 7 und 8):

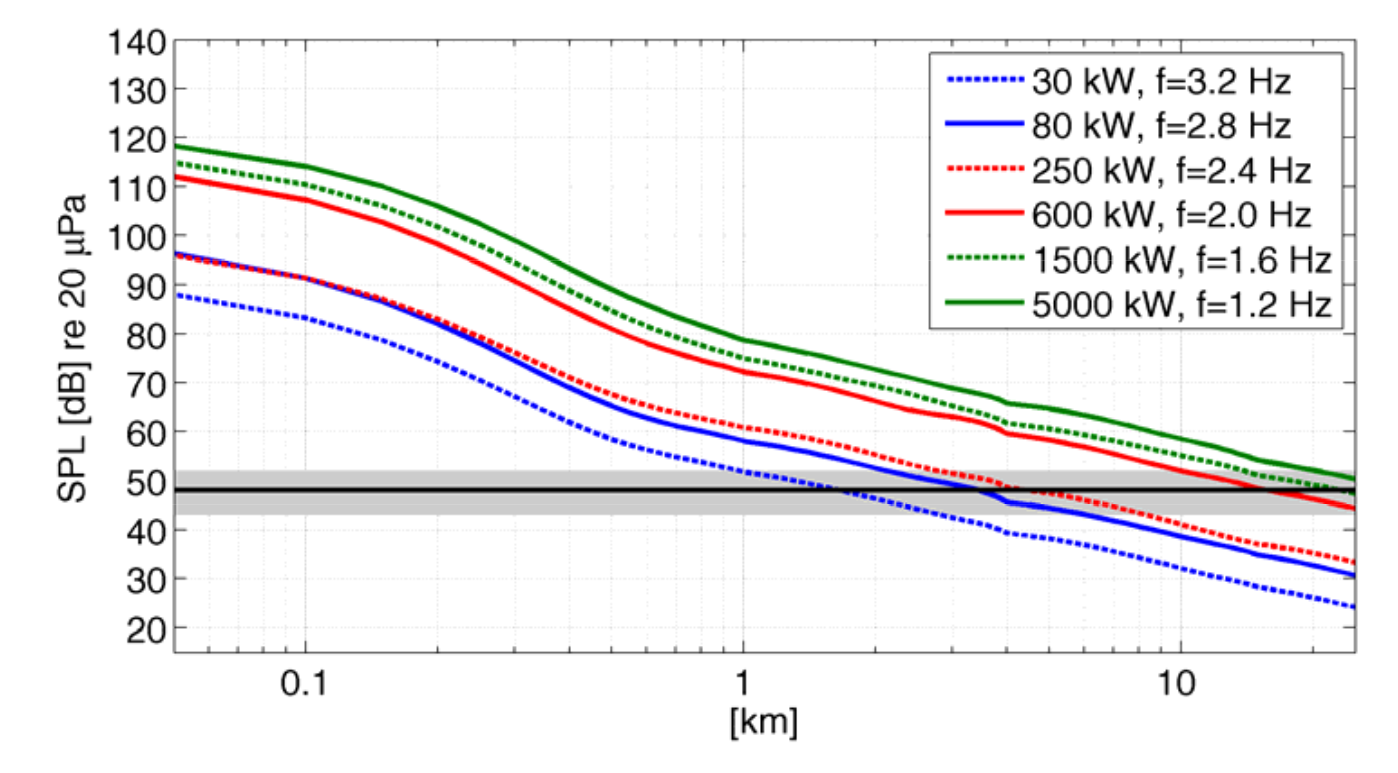
Abbildung 5: Modellrechnungen des Schalldruckpegels der 2. BPH für unterschiedliche Windradtypen (Ceranna 2009, Abbildung 7)

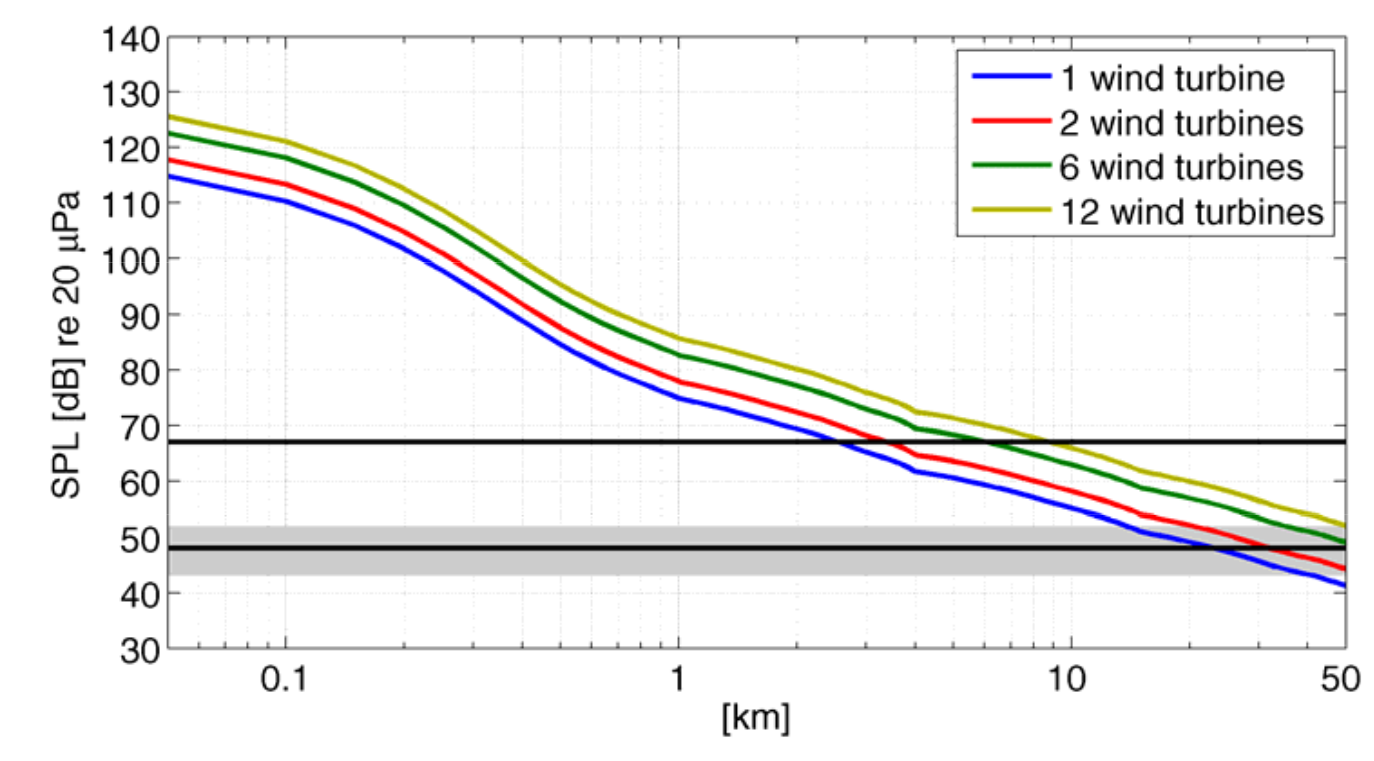
Abbildung 6: Modellrechnungen des Schalldruckpegels der 2. BPH für unterschiedliche Anzahl von WEA in einem Windpark (Ceranna 2009, Abbildung 8)

Auf Webseiten der Windenergiegegner dürften diese beiden Abbildungen zu den meistzitierten Grafiken zählen. Leider sind die dargestellten Schalldrücke mindestens um 30dB zu hoch. Schiebt man die Kurven um 30dB nach unten, sind die Schalldrücke bereits in 1km Entfernung im Bereich des Hintergrundrauschens (grauer Balken). Tatsächlich könnten die Schalldrücke noch tiefer liegen, da auch die Windradtechnik seit den BGR-Messungen von 2004 Fortschritte gemacht hat, und moderne Windräder niedrigere Schallemissionen pro MW-Nennleistung verursachen. Außerdem kommt noch einen Normierungsfehler dazu, da das von Ceranna vermessene Windrad zwei Generatoren hatte (200kW und 660kW). Bei 26rpm ist der große Generator aktiv und das Windrad leistete 660kW (vgl. Diskussionsseite BGR-Studie). Durch die Normierung des Modells auf 200kW statt korrekt 660kW erhöhen sich die errechneten Modellwerte für stärkere Windenergieanlagen um 5dB.

Noch als Radbemerkung sei erwähnt, dass die Modellrechnungen für Windparks bei kleinen Abständen ziemlich sinnfrei sind. Es gibt bei einem Windpark mit 12 Anlagen sicherlich keinen Punkt an dem man zu allen Windrädern einen Abstand von z.B. 200m hat.

Fazit

Es ist offensichtlich, dass die Schalldruckangaben der BGR falsch sind. Trotzdem gibt es bisher keine Richtigstellung von Seiten der BGR. Dies ist sehr bedauerlich, da die Diskrepanz zu Messungen der Umweltämter bis heute von Windkraftgegnern ausgeschlachtet wird, um Zweifel an der Rechtschaffenheit der Umweltämter zu streuen (vgl. Windwahn.com: Spannender Diskurs zur unterschiedlichen Qualität der Messungen von LUBW und BGR- zuletzt abgerufen 13.08.2020). Ich habe Herrn Ceranna mehrfach auf derartige Diskussionen hingewiesen, ohne eine Anwort zu erhalten.

Viele sehen in Fake-News einen gefährlichen Angriff auf die Demokratie. In der Wissenschaft kann und soll man sich streiten. Man kann Zahlen unterschiedlich interpretieren und werten. Aber offensichtlich falsche Zahlen haben im Wissenschaftsbetrieb keinen Platz!